17073번: 나무 위의 빗물
첫째 줄에 트리의 노드의 수 N과 1번 노드에 고인 물의 양을 의미하는 정수 W가 주어진다. (2 ≤ N ≤ 500,000, 1 ≤ W ≤ 109) 다음 N-1줄에 걸쳐, 트리에 존재하는 간선의 정보가 U V의 형태로 주어진다
www.acmicpc.net
✅ 문제 설명
- 1번 정점(루트)에 W만큼의 물이 고여있고, 다른 정점들에는 물이 고여있지 않은 상태입니다.
- 이때 모든 정점은 아래의 작업을 매초 마다 반복합니다.
- 물을 가지고 있으며, 자식 정점이 있다면 자식 정점 중 하나를 골라 물을 1 준다. 자식 정점이 여러 개라면 동일한 확률로 그 중 하나를 고른다.
- 만약 부모 정점이 자신에게 물을 흘려보냈다면 받아서 쌓아 둔다.
- 위 작업이 다 끝나서 더 이상 물이 움직이지 않을 때, 정점 i에 쌓인 물의 기대값을 Pi라 하면 Pi가 0보다 큰 정점들(=리프노드들)에 대해서 Pi의 평균을 구하는 문제입니다.
처음에는 문제가 잘 이해가 되지않아서 아래와 같이 모든 수를 그려보다가 걷잡을 수 없이 늘어가는 결과들을 보면서 아.. 모든 경우의 수를 따지는건 아니구나라는 생각을 했습니다.
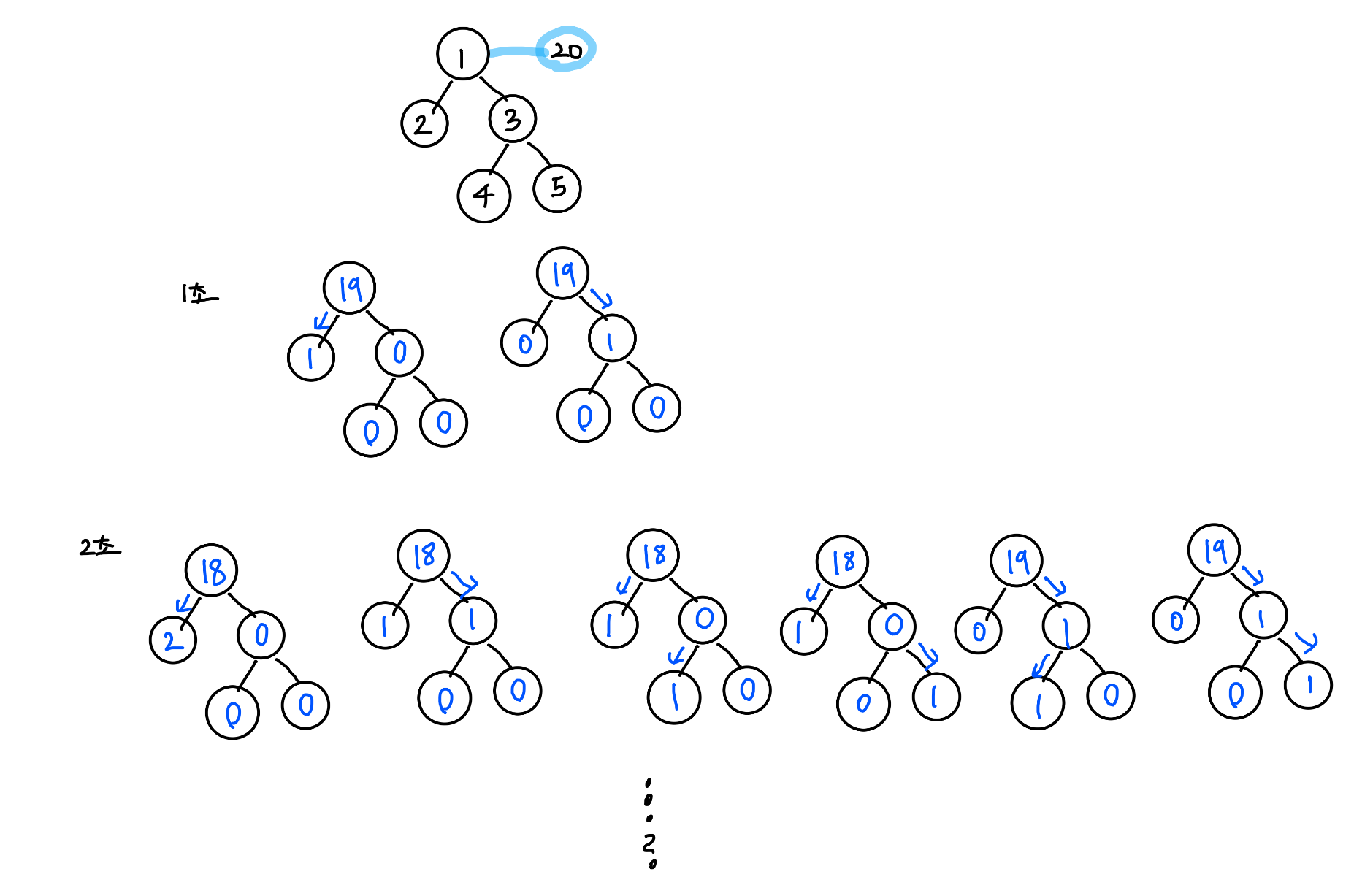
이후에, 아니 그럼 기댓값을 어떻게 구할까..? 생각을 했습니다.
문제에서 주어진 종료 조건을 다시보면 다음과 같습니다.
더 이상 물이 움직이지 않을 때, 정점 i에 쌓인 물의 기대값을 Pi라 하면 Pi가 0보다 큰 정점들(=리프노드들)에 대해서 Pi의 평균을 구해라
물이 더 이상 움직이지 않는다는 뜻은 루트에 있던 물 W가 아래로 타고타고 내려가 모든 물이 리프노드들에 전달이 되었다는 것을 말합니다. 따라서 리프노드들의 Pi(=기대값)를 구하고, 평균을 내주면 되는 문제입니다.

자식 정점이 여러 개라면 동일한 확률로 그 중 하나를 골라 물을 내려보내기 때문에 물이 각 리프노드로 갈 확률을 구하면 각각 노드2는 1/2, 노드4는 1/4, 노드5는 1/4가 됩니다. 여기서 1번 노드에 주어졌던 물의 총량 W를 곱하면 각 리프노드에 물이 얼마나 갈지 기댓값을 뜻합니다. 그리고 평균을 내기 위해 리프노드의 개수를 나눠줍니다.
(1/3) *(20*(1/2+1/4+1/4))가 정답이 되는데 사실 1/2+1/4+1/4 각각의 리프노드로 물이 갈 확률을 다 합치면 1이 되기 때문에 (1/3)*20만 계산해주면 됩니다. 즉 (1/(리프노드의 개수))*W를 수행하면 되기 때문에 결국은 리프노드의 개수를 구하는 문제로 귀결됩니다.
✅ 접근 방식
실패한 접근 방식
처음에 저는 dfs(재귀적구현)로 트리를 탐색하면서 leaf_node의 수를 새려고 하였습니다.
위 접근 방식으로 풀이한 코드는 다음과 같았습니다.
# 나무 위의 빗물
import sys
sys.setrecursionlimit(10 ** 5)
def dfs(i):
visited[i] = 1
global leaf_node
flag = True
for child in tree[i]:
if visited[child] == 0:
flag = False
dfs(child)
if flag:
leaf_node += 1
N, W = map(int, sys.stdin.readline().split())
tree = [[] for _ in range(N + 1)]
for i in range(N - 1):
U, V = map(int, sys.stdin.readline().split())
tree[U].append(V)
tree[V].append(U)
leaf_node = 0
visited = [0 for _ in range(N + 1)]
dfs(1)
print(W/leaf_node)위와 같은 방법으로 풀었을 때, sys.setrecursionlimit(10 ** 5)로 하면 RecursionError가 나고, sys.setrecursionlimit(10 ** 6)으로 하면 메모리 초과가 났었습니다.
성공한 접근 방식
메모리 초과가 나는 것을 막기 위해 stack을 이용하여 dfs를 구현해 리프노드의 개수를 계산했더니 성공할 수 있었습니다.

코드는 다음과 같습니다.
import sys
def stack_dfs(start):
stack = [start]
leaf_node = 0
while stack:
current_node = stack.pop()
visited[current_node] = 1
flag = True
for child in tree[current_node]:
if visited[child] == 0:
stack.append(child)
flag = False
if flag:
leaf_node += 1
return leaf_node
N, W = map(int, sys.stdin.readline().split())
tree = [[] for _ in range(N + 1)]
for i in range(N - 1):
U, V = map(int, sys.stdin.readline().split())
tree[U].append(V)
tree[V].append(U)
visited = [0 for _ in range(N + 1)]
leaf_node = stack_dfs(1)
print(W / leaf_node)
✅ 코드 설명
def stack_dfs(start):
stack = [start]
leaf_node = 0
while stack:
current_node = stack.pop()
visited[current_node] = 1
flag = True
for child in tree[current_node]:
if visited[child] == 0:
stack.append(child)
flag = False
if flag:
leaf_node += 1
return leaf_node스택을 이용해 dfs를 구현하였습니다. flag 변수를 두어서 만약 인접노드가 다 방문한 노드라면 if visited[child]==0: 안의 코드를 실행시키지 못하니까 flag = True일테고, 이 경우 leaf_node라고 판단하여 leaf_node +=1로 리프노드의 수를 카운팅해줍니다.
N, W = map(int, sys.stdin.readline().split())
tree = [[] for _ in range(N + 1)]
for i in range(N - 1):
U, V = map(int, sys.stdin.readline().split())
tree[U].append(V)
tree[V].append(U)
visited = [0 for _ in range(N + 1)]
leaf_node = stack_dfs(1)
print(W / leaf_node)입력을 받아 인접리스트 tree를 구현하고, 방문 여부를 확인할 visited 배열을 다 0으로 초기화해둡니다.
이후 앞에서 정의한 stack_dfs의 인자값에 루트인 1을 넘겨주고 leaf_node(=리프노드의 개수)를 반환받습니다.
leaf_node의 수를 알았으니, 이를 W에 나눠주면 해당 값이 0이 아닌 Pi의 평균이 됩니다.
✅ 최종 코드
import sys
def stack_dfs(start):
stack = [start]
leaf_node = 0
while stack:
current_node = stack.pop()
visited[current_node] = 1
flag = True
for child in tree[current_node]:
if visited[child] == 0:
stack.append(child)
flag = False
if flag:
leaf_node += 1
return leaf_node
N, W = map(int, sys.stdin.readline().split())
tree = [[] for _ in range(N + 1)]
for i in range(N - 1):
U, V = map(int, sys.stdin.readline().split())
tree[U].append(V)
tree[V].append(U)
visited = [0 for _ in range(N + 1)]
leaf_node = stack_dfs(1)
print(W / leaf_node)
❇️ 코멘트
- 확실히 예전보다 트리 문제를 푸는 데 수월해졌으나, 아직 dfs를 재귀적으로만 짜는데 익숙해서 메모리 초과가 자주 발생하는 것 같습니다. 따라서 저번 포스팅에서 언급했던 dfs, bfs를 어떻게 구현할 수 있는 지 여러 방법을 알아보고 정리한뒤 포스팅하고, 이제는 트리 부분을 마무리 하려합니다.
'알고리즘 > 백준' 카테고리의 다른 글
| [BOJ_11000] 강의실 배정 (python) (0) | 2024.05.28 |
|---|---|
| [BOJ_2015] 수들의 합 4 (python) (0) | 2024.05.27 |
| [BOJ_2263] 트리의 순회 (1) | 2024.01.13 |
| [BOJ_4256] 트리 (1) | 2024.01.12 |
| [BOJ_1967] 트리의 지름 (2) | 2023.12.31 |
